The physics of floating pyramids

An unexpected result is reported here.

Results just in from an experiment that levitated open-bottomed paper pyramids on gusts of air reveal a curious phenomenon: When it comes to drifting through the air, top-heavy designs are more stable than bottom-heavy ones. The finding may lead to robots that fly not like insects or birds but like jellyfish.
......
The researchers placed hollow paper pyramids inside the cylinder. The objects were about 1 to 5 centimeters high and were made of tissue paper or letter paper on carbon fiber supports, like tiny homemade kites. Physicist Bin Liu led the experiments, attaching a beadlike weight to a post running down the center of the pyramid and changing the height of the bead to give the object a different center of mass. Common sense says that the pyramid should be most stable when the bead is at the bottom of the post, like ballast in the hold of a ship. But when the team released the pyramids over the subwoofer, the opposite was true: the bottom-heavy pyramids were likely to flip over and fall, whereas the top-heavy ones remained upright and continued to hover (see first video), the group reports in an upcoming issue of Physical Review Letters.
......

The team suspected that the effect was due to swirls of air that develop along the pyramid's sides. To see the swirls in action, Zhang's group examined a two-dimensional version of the pyramid experiment in water. They placed upside-down V shapes into a pan of water and rocked it to create currents. As the water ran past the V, it created tiny whirlpools at the ends of the V's two legs (see second video). These swirls pushed away from the upside-down V, moving downward, which exerted an upward force on the V-the same mechanism that creates lift in the pyramids.

If the V was tilted, however, the swirls went in different directions: Those on the higher leg shoved it sideways, while the lower leg got a weaker upward push. This would straighten the upside-down V. Team member Leif Ristroph showed that the same sorts of swirls roll off the sides of the pyramids: They push the pyramid upright as long as the center of mass is above the tilted-up side, much in the same way that you can balance a vertical stick on the end of your finger by moving the bottom of the stick in the direction of the tilt, Zhang says. For bottom-heavy pyramids, this same mechanism causes them to flip over-it's like moving the top of the stick in the direction of the tilt, encouraging it to fall.

Fun with polymers

http://www.youtube.com/watch?v=vIQpoka8FOk&feature=related

The physics of how bubbles clean dusts

This is an interesting study published in PRL [PRL 107, 074503 (2011)], "It is now accepted that the physical forces in ultrasonic cleaning are due to strongly pulsating bubbles driven by the sound field. Here we have a detailed look at bubble induced cleaning flow by analyzing the transport of an individual particle near an expanding and collapsing bubble. The induced particulate transport is compared with a force balance model. We find two important properties of the flow which explain why bubbles are effectively cleaning: During bubble expansion a strong shear layer loosens the particle from the surface through particle spinning and secondly an unsteady boundary layer generates an attractive force, thus collecting the contamination in the bubble’s close proximity." The following is a review:

A team at the Nanyang Technological University in Singapore led by Claus-Dieter Ohl adapted a technique for creating a bubble where and when they wanted it. They focused a laser pulse up through a glass microscope slide into a strongly absorbing liquid dye. The laser heating caused the bottom layer of the dye to evaporate explosively, forming a hemispherical bubble at the glass surface that grew to tens of microns in radius and then collapsed, all within about 25 microseconds. The team stuck several-micron-diameter plastic beads on the slide surface and immersed them in the dye to mimic dirt particles adhering to a surface. They then recorded video of the beads' motion in response to the bubble.

Physics about Guinness

This time we get to the physics of a kind of Irish beer, Guinness, which catches eyes for the bubbles and colors forming in it.

Look closely at a pint of Guinness and tell me: do the bubbles go up, or do the bubbles go down? Why is the head coloured the way it is? Is foam a gas, liquid or solid? An Irish physicist discusses.
....
The paper referenced in this discussion is "Waves in Guinness" by Marguerite Robinson, A. C. Fowler, A. J. Alexander, and S. B. G. O'Brien [DOI: 10.1063/1.2929369; free PDF]. And yes, it is rather intense reading, unless you are a fluid physicist or an astronomer. [http://www.guardian.co.uk/science/punctuated-equilibrium/2011/aug/02/1]

Cool Water Fountain

Here is a show of a very cute water fountain in Japan.

Think about the physics in it !

How do wings work ?

This is an interesting article from the wonderful journal I posted in my last entry. It tries to poke the usual (even textbook) explanation of how wings work [2003 Phys. Educ. 38: 497].

Now Bernoulli’s equation is quoted, which states that larger velocities imply lower pressures and thus a net upwards pressure force is generated. Bernoulli’s equation is often demonstrated by blowing over a piece of paper held between both hands as demonstrated in figure 2. As air is blown along the upper surface of the sheet of paper it rises and, it is said, this is because the average velocity on the upper surface is greater (caused by blowing) than on the lower surface (where the air is more
or less at rest). According to Bernoulli’s equation this should mean that the pressure must be lower above the paper, causing lift. The above explanation is extremely widespread. It can be found in many textbooks and, to my knowledge, it is also used in the RAF’s instruction manuals. The problem is that, while it does contain a grain of truth, it is incorrect in a number of key places.

What’s wrong with the ‘popular’ explanation?
The distance argument;
The ‘equal time’ argument;
The Bernoulli demonstration.

Next, examine a particle moving along a curved streamline as shown in figure 7. For simplicity we can assume that the particle’s speed is constant3. Because the particle is changing direction there must exist a centripetal force acting normal to the direction of motion. This force can only be generated by pressure differences (all other forces are ignored), which implies that the pressure on one side of the particle is greater than that on the other. In other words, if a streamline is curved, there must be a pressure gradient across the streamline, with the pressure increasing in the direction away from the centre of curvature.

Study blames plasma flow for quiet sun

Our sun is maintained by converting gravitational energy into electromagnetic energy (e.g., visible and invisible radiations). The temperature is so high that the solar matter exists only in gas of light ions and electrons. These are charged particles. Their motions may take the form of the so-called 'plasma', which has these charges moving in a coherent and collective way, appearing as waves. The dynamics are quite nonlinear and intricate. Associated with such plasma, the electromagnetic fields will also change, and have been well known following a very regular pattern. One way to notice this pattern is by counting the intensity of the so-called sunspots, which are caused by pop-ups of strong magnetic energy flow from interior to the surface, like a cork decorated with flares carrying a huge amount of energy that may partly reach the earth. The latest solar cycle peaked in 2001 and was supposed to end in 2008. However, there is something unusual with this cycle: the sun appears too sluggish, with an extra number of spotless days. Now researchers came up with an explanation, which seems under debate [http://www.wired.com/wiredscience/2011/03/spotless-sun-model/]:

Now, Dibyendu Nandy of the Indian Institute of Science Education and Research and colleagues offer an explanation: A “conveyor belt” of plasma inside the sun ran quickly at first and then slowed down.

Nandy and colleagues at Montana State University and the Harvard-Smithsonian Center for Astrophysics ran a computer simulation of magnetic flow inside the sun for 210 sunspot cycles. They randomly varied the speed of plasma flow around a loop called the meridional circulation, which carries magnetic fields from the sun’s interior to its surface and from the equator to the poles.

Observations suggest that the fastest flow runs around 22 meters per second (49 miles per hour). Nandy’s model looked at speeds between 15 and 30 meters per second (33 to 67 miles per hour).

The model found that a fast flow followed by a slow flow reproduced both the weak magnetic field and the dearth of sunspots observed in the last solar minimum.

....

Unfortunately, observations of the sun’s surface seem to directly contradict the new model.

“We’re in this quandary, this clash between theory and observations,” said NASA astronomer David Hathaway, who analyzed 13 years of data from the Solar and Heliospheric Observatory (SOHO) that tracked the movement of charged material near the surface of the sun.

Hathaway agrees that a fast flow can cause weak magnetic fields and fewer sunspots. But his observations, published March 12, 2010 in Science, suggest that the meridional flow was slow in the first half of the last solar cycle, from about 1996 to 2000. Only after the solar maximum did the flow speed up.

“That’s where there’s a problem,” Hathaway said. “We see one thing, they want the opposite to explain the observations.”

Nandy and colleagues point out that the SOHO observations only see plasma moving at the surface of the sun, not in the deep interior where sunspots are born. The surface flows might not reflect what’s going on underneath, he says.

“In an analogy that you might be able to relate to, one could ask, do ripples on the surface of the sea indicate how ocean currents determine the migration of aquatic animals deeper inside?” Nandy said.

Hathaway argues that changes in the surface should be transmitted to the interior at the speed of sound, and should reach the creation zone in half an hour or less. The disagreement between theory and data means there must be a problem with the models, he says.

Trends: Climate Modelling

Brad Marston [Physics, 4:20(2011)] suggests physicists think about tackling climate problems, e.g., how to model climate. He wrote, "In this article, I discuss specific advances in nonequilibrium statistical physics that have direct applications on efforts to understand and predict the climate. (For an excellent introduction to the general science of climate change, see David Archer’s Global Warming: Understanding the Forecast [3].) But first, let’s look at the sort of question a statistical description of the climate system would be expected to answer."

Couterflow

This Letter addresses a practical problem that is encountered in, for example, a recent oil gushing in Mexico Gulf. To 'top kill' the oil well, one may pump "mud" from above to suppress the welling from bottom. However, in this "top kill", one needs consider an issue as described in the mentioned Letter, the so-called "Helmholtz instability", namely, "Dense fluids, i.e., mineral suspensions called ‘‘mud’’ [1,2], are introduced into oil wells to provide hydrostatic pressure to offset hydrocarbon (oil and gas) fluid pressure in deep formations, stopping upward flow and reducing the fluid pressure at the surface to near ambient. If hydrocarbon is flowing upward in the well, there is a counterflow between the upwelling hydrocarbon and the descending mud. Successful top kill requires that the mud descend despite this counterflow. However, upwelling at speeds > 1m/s, as in the uncontrolled Macondo well ‘‘blowout’’ in the Gulf of Mexico in 2010, may lead to a Kelvin- Helmholtz instability [3]."[PRL 106, 058301 (2011)] How to avoid the instability ? Suggested to use viscoelastic materials.

Nonlinear dynamics are not easy !!

This review [http://www.nature.com/nature/journal/v470/n7335/full/470475a.html?WT.ec_id=NATURE-20110224#/references] explains why I claim that !

The formal problem of the stability of rotating flow was first addressed by Lord Rayleigh in the late nineteenth century⁷. Rayleigh found that if the rotational velocity of a fluid decreases more rapidly with radius than the reciprocal of the distance from the axis of rotation, such a system is unstable to infinitesimal perturbations. Astrophysical disks, by this criterion, should be stable. But Rayleigh's analysis was restricted to vanishingly small disturbances, and the geometrical shape of the perturbations was in the form of rings with cylindrical symmetry. It is still not known what types of flow that are formally stable by this Rayleigh criterion might still be unstable to more general forms of disturbance; it is known, however, that some types of Rayleigh-stable flow certainly can be destabilized^{4, 8}. The issue of interest is whether the rotation of an astrophysical gas disk about a central mass falls into this unstable category.

This problem can be investigated in the laboratory by studying what is known as Couette flow. In a Couette apparatus, water is confined to flow in the space between two coaxial cylinders. There should be no motion along the central axis, only rotational flow about the axis. The cylinders rotate independently of one another, so that small frictional viscous forces near the cylindrical walls will set up a hydrodynamical flow in which the rotational velocity depends on the distance from the rotation axis. By choosing the rotational velocities of the rotating cylinders appropriately, a small section of an astrophysical disk can be mimicked in the laboratory. In such a disk, the flow velocity is inversely proportional to the square root of the distance from the centre, a pattern known as Keplerian flow. The question to be answered is whether Keplerian flow, formally stable by the Rayleigh criterion, actually breaks down into turbulence.
......

It is this question that Paoletti and Lathrop¹ have sought to address. When a Couette flow becomes turbulent, one of the consequences is a greatly enhanced outward flux of angular momentum, which is imparted to the outer cylinder in the form of a torque. In their experiment, the authors measure this torque directly. An earlier investigation⁹ had claimed to detect this torque, but the new experiment¹ was conducted under conditions in which (undesirable) viscous effects were more effectively minimized.

Close on the heels of Paoletti and Lathrop's claim, however, comes a report by Schartman et al.¹⁰ on a related experiment. These investigators found no transition to turbulence for Keplerian flow with the same controlled level of viscosity. This null result was first reported³ in 2006, and the most recent paper maintains its original conclusion that there is no evidence of a turbulent breakdown of Keplerian-like laminar flow for very small values of the viscosity.

Thermofluidic effects in nanochannels

When a fluid is subject to a temperature gradient, a velocity field can be generated, a phenomenon known as convection. It should be noticed that, such phenomena parallel what happens to electrons in a metal: temperature gradient drives electrical current under the name of thermoelectric effect. Now as things can be made smaller and smaller, it becomes an interesting subject to investigate the so-called micro- or nano-fluidic flow: liquid flow through a micro-size or nano-size channel. In this study by researchers from Hong Kong [PRL 105, 174501 (2010)], they used molecular dynamics simulations to examine a nano fluid housed in a nano-channel with particularly designed walls: the wall consists of two parts, the left and the right one, with respective surface energies, and a temperature gradient is held symmetric with respect to the border between the left and right wall. Their study showed that, an asymmetric flow can be generated with this temperature gradient provided the variance of surface energies is big enough. This is funny and many possibilities can be imagined to broaden their studies.

Special relativity comes to the help

In an ideal non-relativistic fluid without viscosity no circulation can be generated from none. This fact makes a challenge in cosmology: the genesis of the magnetic field ubiquitous to galaxies. In this Letter [PRL 105, 095005 (2010)], however, the authors were able to show how this theorem can break because of special relativity. They show that, even for an ideal dynamic fluid, circulation can arise naturally without the help of ad hoc commotions.

We demonstrate that a purely ideal mechanism, originating in the space-time distortion caused by the demands of special relativity, can break the topological constraint (leading to helicity conservation) that would forbid the emergence of a magnetic field (a generalized vorticity) in an ideal nonrelativistic dynamics. The new mechanism, arising from the interaction between the inhomogeneous flow fields and
inhomogeneous entropy, is universal and can provide a finite seed even for mildly relativistic flows.

confined water

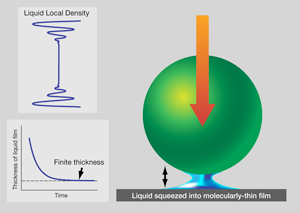The properties of water under conventional conditions are largely known to scientists. But those under unusual cases are rarely revealed. One example is, what happens to the viscosity and elasticity of water confined to two solids in thin layer of nanometer? According to a recent study[1], there may happen a solid-like transition with respect to the rate at which the two solids approach each other, that is, elasticity increases while viscosity decreases.
[1]Phys. Rev. Lett. 105, 106101 (2010)

Schematic illustration of a confined fluid. Imagine that a liquid droplet is placed between a ball and a flat surface, and a ball is allowed to fall (right panel) onto it. When the thickness of the liquid is plotted schematically against time after the ball begins to fall, the film thickness remains finite at equilibrium (bottom left panel). This is because fluid tends to layer parallel to the solid surfaces. When the local liquid density is plotted against the distance between the solid boundaries, it shows decaying oscillations with a period of about a molecular dimension (top left panel). When these density waves shown in the bottom panel come sufficiently close to interfere with one another, the liquid can support force at equilibrium.

Imaging the coffee blend with cream

This is so cool !
http://www.insidescience.org/research/coffee_cup_secrets

Bubbles to penetrate cell membranes

Fluid dynamics concerning bubbles are complex and interesting. When a bubble collapses, flow jet might be created at high speed. When it hits on something, the force can be quite large. Here is a delicate experiment that explores this phenomenon to practical ends [Phys. Rev. Lett. 105, 078101 (2010)].

Figure caption: The timed expansion and collapse of two bubbles creates a liquid jet that can penetrate a fine hole in the membrane of a cell. From left to right: A laser (green circle) focused inside a water bath locally vaporizes the liquid, creating an expanding bubble (light blue). Just after the first bubble reaches its maximum size, a second laser (red circle) generates another bubble. As the second bubble expands and the first bubble collapses, a rush of liquid forms along the vertical line (pink arrow) between the two, creating a high-speed liquid jet that accelerates toward the cell with enough force to penetrate the membrane.

What does physics say about the Jobulani ?

The ball created by Adidas for this year's World Cup has its name as 'Jobulani' ? What is special about it ? Listen to the audio of this link.

Fluid close to a wall

The turbulence phenomena have remained a puzzle for hundreds of years. Efforts to resolve it never stop.

The behavior of turbulent fluid motion, particularly in the thin chaotic fluid layers immediately adjacent to solid boundaries, can be difficult to understand or predict. These layers account for up to 50% of the aerodynamic drag on modern airliners and occupy the first 100 meters or so of the atmosphere, thus governing wider meteorological phenomena. The physics of these layers is such that the most important processes occur very close to the solid boundary—the region where accurate measurements and simulations are most challenging. We propose a mathematical model to predict the near-wall turbulence given only large-scale information from the outer boundary layer region. This predictive capability may enable new strategies for the control of turbulence and may provide a basis for improved engineering and weather prediction simulations.

Science 9 July 2010:
Vol. 329. no. 5988, pp. 193 - 196
DOI: 10.1126/science.1188765

soccer balls spinning in the air

The World Cup this round is now near its climax. I'm not a soccer fan, though it is my interest to know how the soccer balls traverse the air. One finds here a good and terse essay on this. It talks of how the trajectory of a soccer through the air is affected by the drag force and Magnus force, both of which are of course exterted by the air. An exact solution of such problem is only numerically or experimentally possible. Even today, after nearly three centuries since Euler equation, some very fundamental issues as regards the transition from laminar and turbulent flow are not concluded.

Supersonic jet produced when a marble is dropped in a liquid

For imaginative and inquiring minds, even very familiar daily events may contain some totally unexpected shocks, which give them great pleasures. Every one may think he is quite conversant with what might happen when he throws a stone in a basin of water. But, any way, if you read this interesting piece of work, you'll still feel surprised and may proclaim 'O, I did not anticipate this at all !' This kind of work should always be holy in themselves. They challenge common knowledge and refreshes minds and refuels one's passion and curiosity. Now read a review of it.

When scientists speak of a “jet” they are usually referring to a fast flowing column of material, typically air or water. These jets range from the mundane, like water rushing out of a hose, to the exotic, such as the relativistic plasma jets that beam out from quasars or monster black holes. A turbo-jet, for example, pushes an aircraft forward using the supersonic thrust of air that streams out of the back of the engine.

Writing in Physical Review Letters, Stephan Gekle and colleagues at the University of Twente, The Netherlands, in collaboration with the Universidad de Sevilla, Spain, have found a supersonic jet in a surprising place: the collapsing splash from an object falling into water [1]. Their general setup is easy to reproduce by dropping a marble into a deep bowl of water (a billiard ball into a full bucket works even better). This effort is rewarded with not one, but three jets (see Fig.1): First, one of upward streaming supersonic air, followed by an obvious upward jet of water, along with a less evident downward jet of water toward the marble. Although Gekle et al. perform a more controlled experiment—they pull a disk downward through the liquid surface at a controlled speed—the general features of what they find are the same. Moreover, the disk enables Gekle et al. to have good control of the experimental conditions.

In the kitchen version of the experiment, the marble creates a crown-shaped splash and crater as it falls into the liquid. The crater deepens to the point at which the walls start to contract. This is due to both the weight of the water outside and possibly surface tension, both of which create pressure gradients that force the collapse. Air inside this collapsing neck must escape upward or downward as the neck approaches pinch-off. It is in this escaping air that Gekle et al. found supersonic velocities—the first jet in this simple experiment (see Video 1).

The shape of the neck plays an interesting role. As the air escapes through the neck, right before the neck closes, it is accelerated to supersonic speeds as it is driven by high pressures from the collapsing cavity below to low pressures in the air above the water’s surface. Engineers have designed a similar process and shape into the convergent-divergent nozzle (or, De Laval nozzle) that is used as the exhaust port in many rocket engines. In our situation, however, the nozzle forms naturally and is quickly changing shape.

At the moment of pinch-off, very large pressures accompany the impact of the water surface on itself. In fact, the pinch-off is a type of near singularity where nearly all observables—velocities, surface curvatures, pressure gradients, etc.,—become very large [2]. Consequently, just after the pinch-off, large pressures accelerate the water upward and downward to very high velocities [3, 4]. This drives two spikes of liquid—called rebound jets—up above the water surface and another one downward into the cavity following the marble. These are our second and third jets produced by this experiment. In a low viscosity fluid such as water, the jets often quickly break up into a spray of droplets. Each of these fission events also involves a near singular pinch-off of a fluid neck [2]. In fact, there are cases where the upward spray goes higher than the initial height of the dropped marble [5].

In each case these jets are the consequence of the kinetic energy density locally rapidly rising. The analysis of these processes involves the interplay of inertia and in some cases surface tension. The root cause of these self-focusing events is that the surface is changing its topology. When the crater collapses, the surface cleaves from one sheet to one sheet plus a bubble. These high velocities (and high surface curvatures) all occur right around the time of pinch-off. Other examples where a change in topology is accompanied by divergent observables include the reconnection of quantized vortices in a superfluid [6], the formation of black holes in numerical studies of general relativity [7], crater collapse and jet formation in capillary waves [2], and the coalescence of droplets [8].

In many of these situations the rapid divergence has a small length scale cutoff because there is a crossover to a different balance of forces (e.g., at really small length scales, capillary action and the molecular structure of the fluid matters). In such cases, we speak of a near singularity rather than a singularity. For instance, viscosity, the speed of sound, or the speed of light might cap some near singularities. One is tempted to generalize that near-singular behavior may usually be present in any change in topology. In some of the examples above it is clear that the system, if forced, produces a local region of high curvature (corners) on the interface that is undergoing topology change. It is fascinating that such an ordinary event as dropping a stone into a pond holds such richness.

References

1. S. Gekle, I. R. Peters, J. M. Gordillo, D. van der Meer, and D. Lohse, Phys. Rev. Lett. 104, 024501 (2010).
2. B. W. Zeff, B. Kleber, J. Fineberg, and D. P. Lathrop, Nature 403, 401 (2000).
3. J. Eggers and E. Villermaux, Rep. Prog. Phys. 71, 036601 (2008).
4. S. Gekle, J. M. Gordillo, D. van der Meer, and D. Lohse, Phys. Rev. Lett. 102, 034502 (2009).
5. J. E. Hogrefe, N. L. Peffley, C. L. Goodridge, W. T. She, H. G. E. Hentschel, and D. P. Lathrop, Physica D 123, 183 (1998).
6. G. P. Bewley, M. S. Paoletti, K. R. Sreenivasan, and D. P. Lathrop, Proc. Nat. Acad. Sci. USA 105, 13707 (2008).
7. M. W. Chopuik, Phys. Rev. Lett. 70, 9 (1993).
8. J. Eggers, J. R. Lister, and H. A. Stone, Fluid Mech. 401, 293 (1999)